Lage von Gerade und Ebene

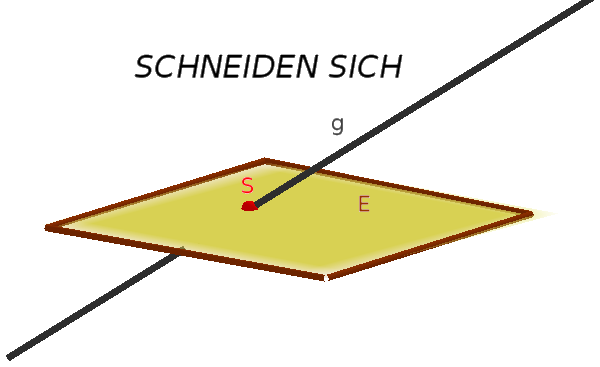
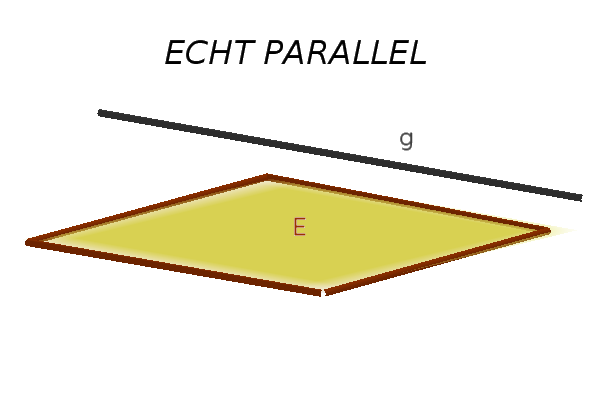
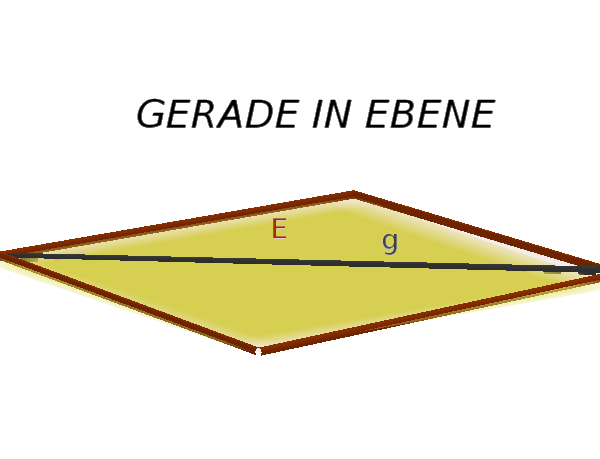
Man unterscheidet drei mögliche Lagebeziehungen zwischen einer Geraden $g$ und einer Ebene $E$.

• $g$ und $E$ schneiden sich
  
• $g$ und $E$ sind echt parallel
  
• $g$ liegt in der Ebene $E$
  

Beispiel

$\text{g: } \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$

$\text{E: } 2x+y+2z=-2$

1. Geradengleichung umschreiben

   Der Vektor $\vec{x}$ in der Geradengleichung wird ersetzt durch $\begin{pmatrix} x \\ y \\ z \end{pmatrix}$.

   $\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$

   Jede Zeile entspricht einer Gleichung

   1. $x=\color{red}{2+2r}$
   2. $y=\color{blue}{1-3r}$
   3. $z=\color{green}{1+4r}$

2. $x$, $y$, $z$ einsetzen

   Die einzelnen Gleichungen für $x$, $y$, $z$ können in die Koordinatengleichung der Ebene eingesetzt werden.

   $\text{E: } 2\color{red}{x}+\color{blue}{y}+2\color{green}{z}=-2$

   $2\cdot\color{red}{(2+2r)}$ $+\color{blue}{(1-3r)}$ $+2\cdot\color{green}{(1+4r)}$ $=-2$

   Nun werden die Klammern aufgelöst und die Gleichung nach $r$ umgestellt

   $4+4r+1-3r+2+8r$ $=-2$
   $7+9r=-2\quad|-7$
   $9r=-9\quad|:9$
   $r=-1$

3. Ergebnis deuten

   Da wir ein eindeutiges $r$ rausbekommen haben, müssen sich die Ebene und die Gerade schneiden und man kann den Schnittpunkt berechnen.

   => Gerade $g$ und Ebene $E$ schneiden sich.

   Der Schnittpunkt wrid berechnet, indem man $r=-1$ in die Geradengleichung einsetzt.

   $\begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} + (-1) \cdot \begin{pmatrix} 2 \\ -3 \\ 4 \end{pmatrix}$ $=\begin{pmatrix} 0 \\ 4 \\ -3 \end{pmatrix}$

   => Schnittpunkt $S(0|4|-3)$.