Wertetabelle anlegen
Die Normalparabel besitzt die Funktionsgleichung $f(x)=x^2$. Für $x$ setzen wir jetzt Werte von -3 bis 3 ein.$f(-3)=(-3)^2=9$
$f(-2,5)=(-2,5)^2=6,25$
$f(-2)=(-2)^2=4$
...
$f(3)=3^2=9$
Werte in ein Koordinatensystem eintragen
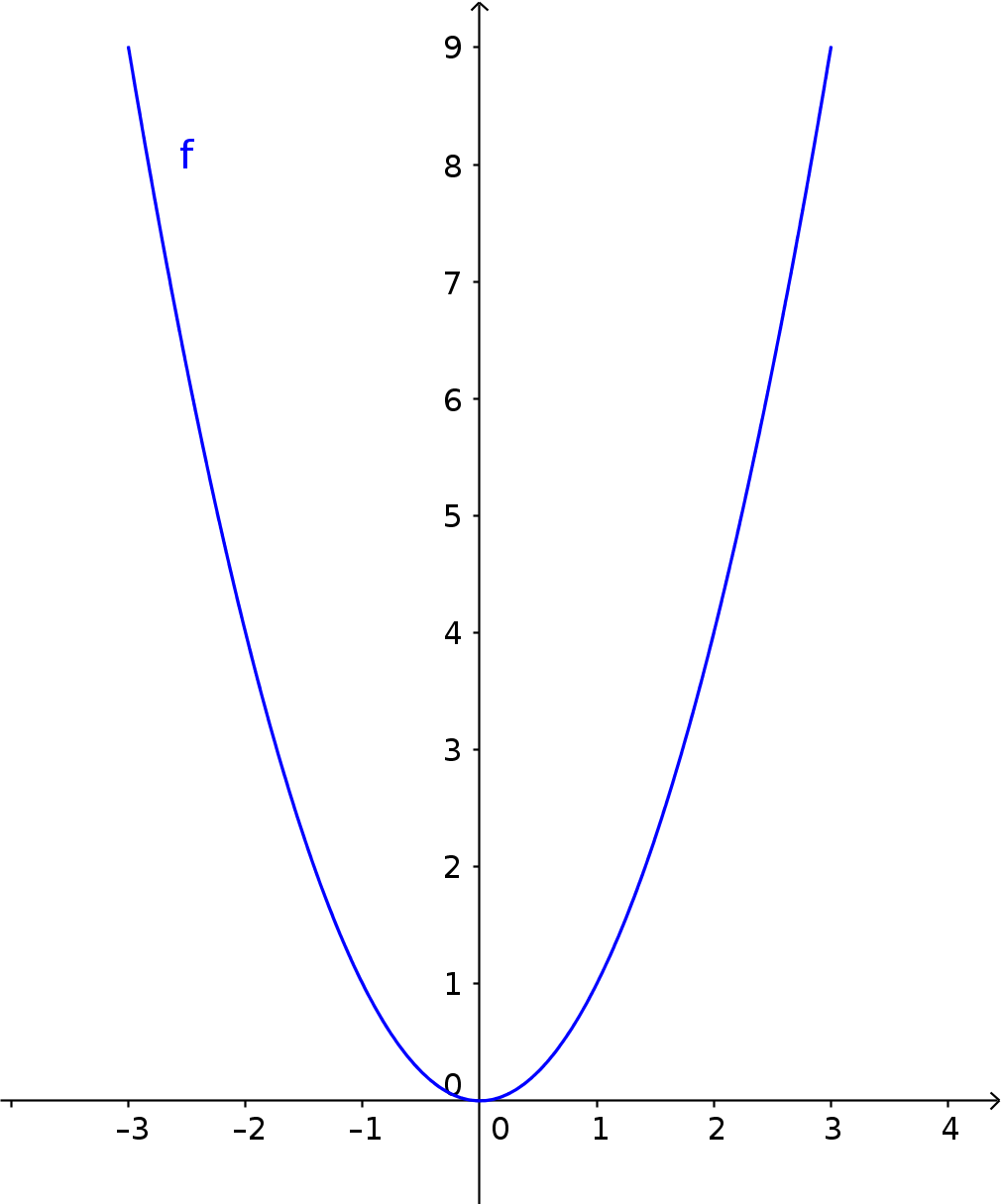
Die Normalparabel ist die einfachste quadratische Funktion. Sie besitzt die Funktionsgleichung $y=x^2$
Zeichne die Normalparabel.
