Die Differenzialrechnung wird bei der Kurvendiskussion benötigt. Hier folgt nur nochmal eine kurze Zusammenfassung.
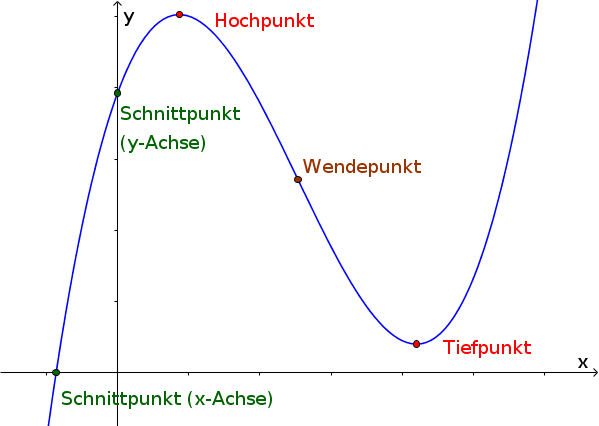
Eine Kurvendiskussion beinhaltet meist folgende Untersuchungen:
| Eigenschaft | Bedingung | |
|---|---|---|
| Achsenschnittpunkte | ||
| Schnittstellen x-Achse (Nullstellen) | $f(x)=0$ | |
| Schnittstelle y-Achse | $f(0)$ berechnen | |
| Symmetrie | ||
| Achsensymmetrie zur y-Achse | $f(-x)=f(x)$ | |
| Punktsymmetrie zum Ursprung | $f(-x)=-f(x)$ | |
| Monotonieverhalten | ||
| monoton steigend | $f'(x)\ge0$ | |
| monoton fallend | $f'(x)\le0$ | |
| streng monoton steigend | $f'(x)>0$ | |
| streng monoton fallend | $f'(x)<0$ | |
| Extrempunkte | ||
| Hochpunkt | $f'(x_E)=0$ und $f''(x_E)<0$ | |
| Tiefpunkt | $f'(x_E)=0$ und $f''(x_E)>0$ | |
| Wendepunkte | ||
| Wendepunkt | $f''(x_W)=0$ und $f'''(x_W)\neq0$ | |