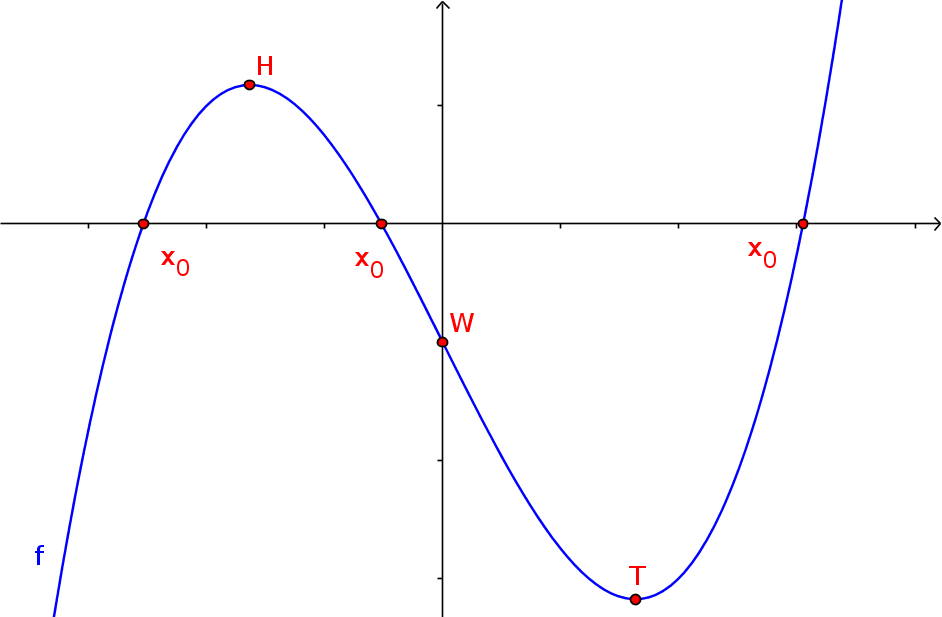
Eine Teilgruppe der rationalen Funktionen sind die ganzrationalen Funktionen oder auch Polynomfunktionen. Sie besitzen eine Gleichung in der Form:
Den Funktionsterm nennt man Polynom und Der Exponent $n$ gibt den Grad des Polynoms an.
Folgende sind typische Funktionsgraphen für Funktionen n-ten Grades:
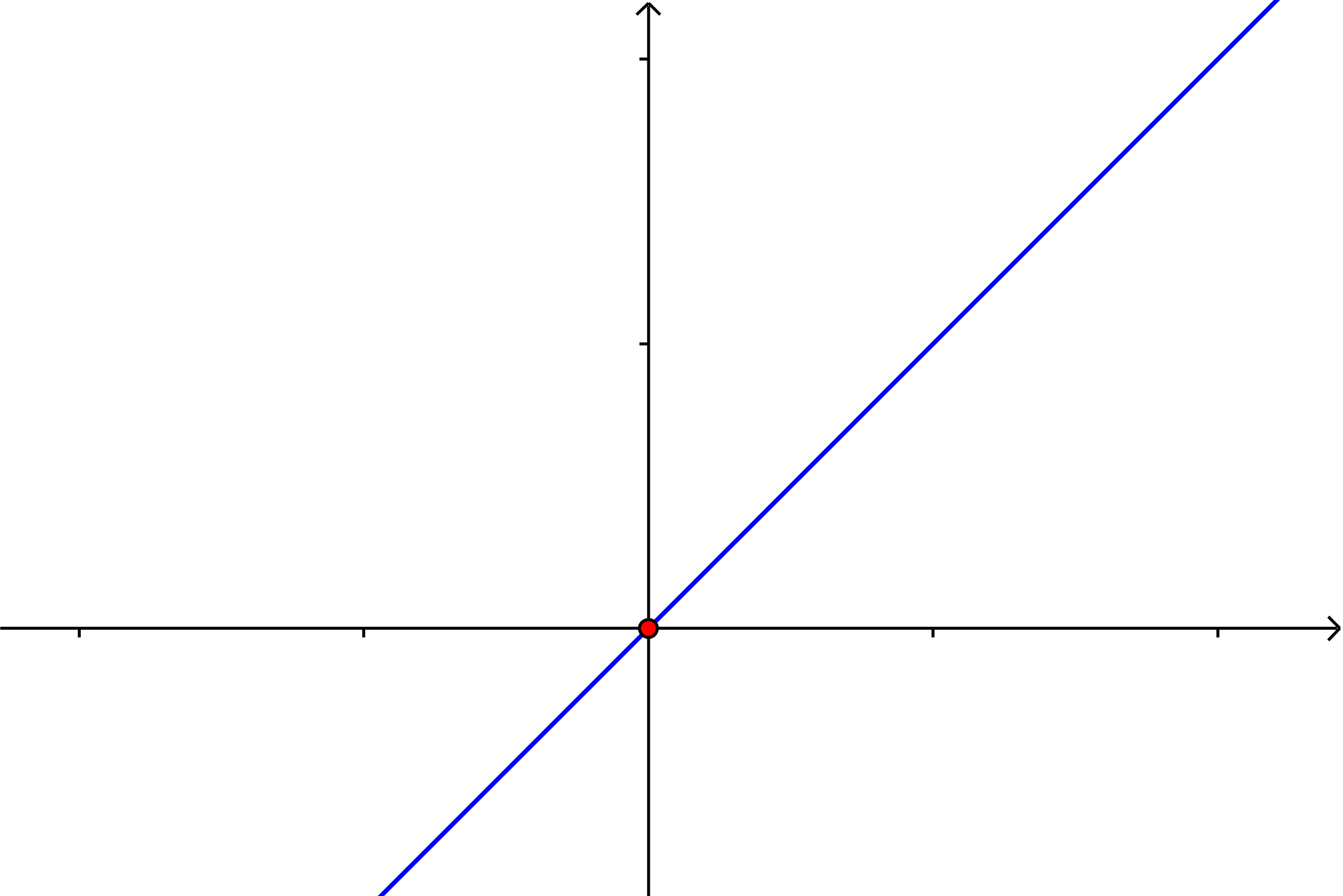
| $n=1$ |
| lineare Funktion* |
$f(x)=x$ |
| $n=2$ |
| quadratische Funktion* |
$f(x)=x^2$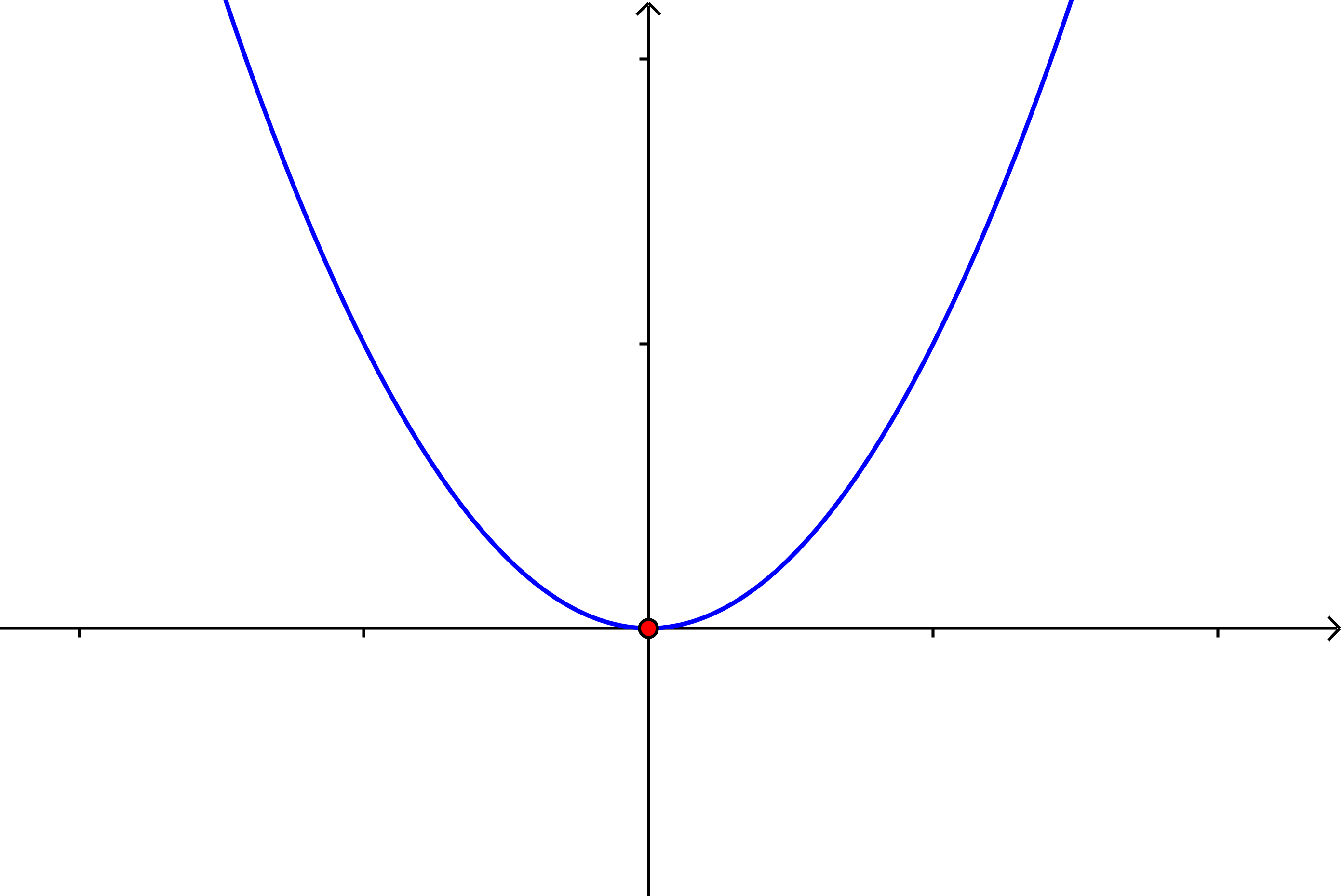 |
| $n=3$ |
| kubische Funktion* |
$f(x)=x^3$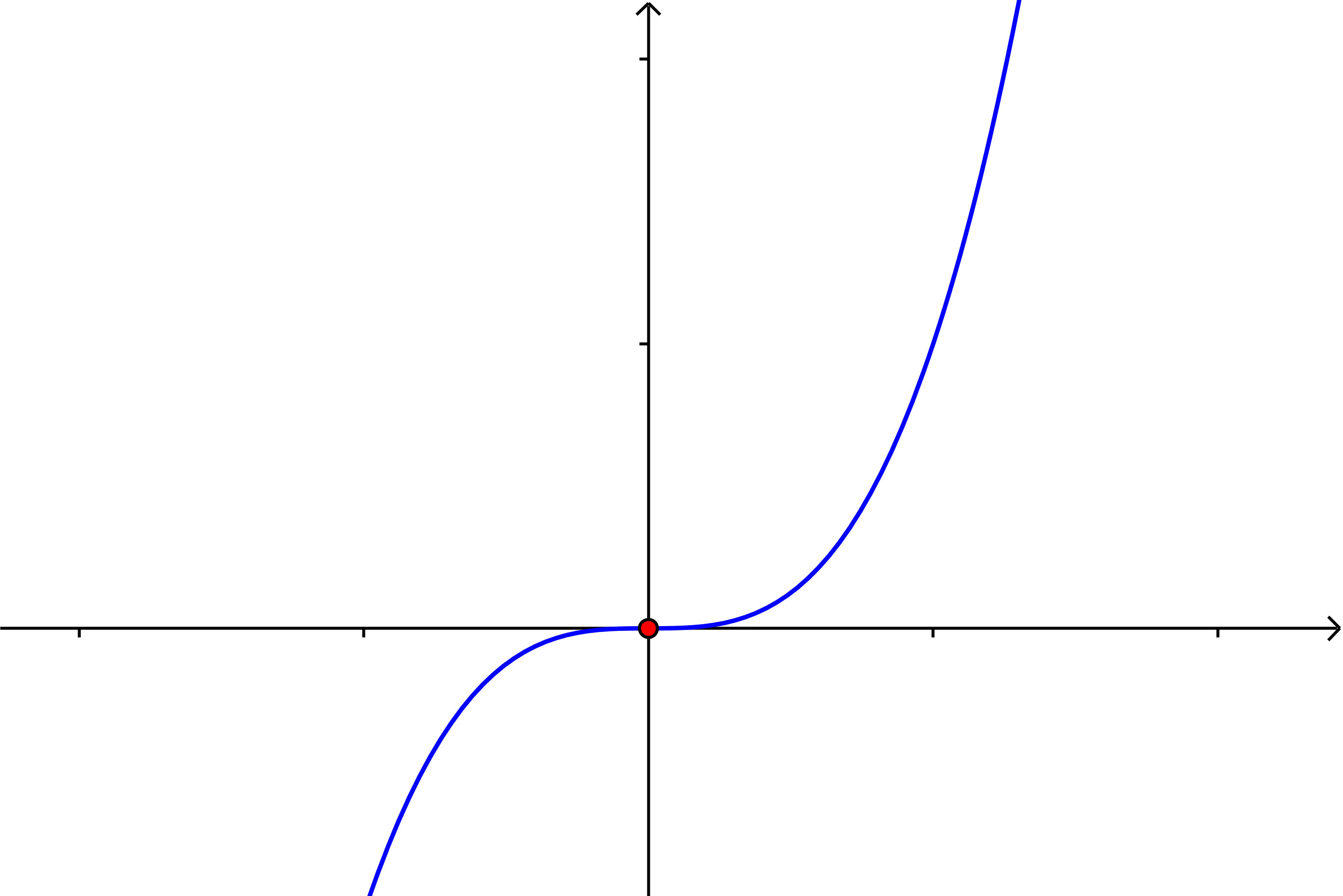 |
* In den Beispielen sind alle Funktionen auch Potenzfunktionen, aber lineare, quadratische und kubische Funktionen sind nur Potenzfunktionen, wenn kein weiterer Summand dahinter steht. Zum Beispiel sind das keine Potenzfunktionen: $f(x)=x+5$ und $f(x)=4x^2-x+3$
Weitere Beispiele für ganzrationale Funktionen sind: